Hexagons are the undisputed best shape. Everyone knows this, and in the RPG space, we love to plan our maps with them.
Hexagons are great because they tesselate infinitely on a flat plane, meaning they also look good on paper and it’s easy to tell where to go next. However, this tesselation does have one downside, this little thing called "the curvature of the earth".
Now, some fantasy worlds solve this problem with creative thinking. Hyperborea is on a flat world with ice-wall edges, the Lost Lands have variable size hexes, Harn claims that the rest of the world is endless ocean. None of these are quite good enough for me. Instead, I’ve decided to combine my history in geometry, redneck engineering and origami to produce what is (in my opinion) the perfect template for an almost perfect hex sphere.
Some Math
This is going to get technical, but I’m going to try to go slow and walk you though my reasoning. If math wigs you out, feel free to scroll past.

As gamers, we’re already pretty familiar with the basics of polyhedrons. We roll the 5 platonic solids without a care in the world, we just call them by different names. D4, D6, D8, D12 and D20. Since every (convex uniform)[1] polyhedron technically maps to a sphere, the question is less about "does it work" and more "does it play nice with hexagons". To this end, let’s look at the Truncated Icosahedron.

You may not know this shape’s name, but you know it. To the Americans, this is a soccer ball, and a football to all the civilized countries. Basically, you cut the corners off a d20 and end up with a 32 sided polygon made of 20 hexs (yay!) and 12 pentagons (boo!).

Through a bit of mathematic trickery though, we can create Goldberg Polyhedrons. I won’t get into the math of Goldberg Polyhedrons, since it’s a bit high level, but suffice to say we can keep truncating that D20 to produce a ball made of 260 hexagons and the same 12 pentagons. Now we’re getting somewhere.
Turning Our Ball into a Map
If you skipped the last section, we took a scalpel to a d20 and made a ball made of 260 hexagons and 12 pentagons. 260 being divisible by 20 is a good thing to have, since we can map 13 of these hexes to each face of the d20, which has a pretty clean unrolled view.

With some creativity, we can instead view the d20 as 10 diamonds of 26. This is better because 10 and 26 have some useful properties. 10 is a good number because it’s the number of digits in a decimal system. 26 is a good number because it happens to line up with the english alphabet. Combining these two facts, we can identify all 260 hexes as some combination of number and letter, from 0A to 9Z.
That leaves us with the 12 pentagons. If we turn the d20 so the north and south poles are on corners, we can identify those as NP and SP, which isn’t exactly the same as everything else, but honestly, how much of your game is taking place at the poles? This leaves us with the 10 around the middle. Since we already split the world into 10 diamonds already, we can just throw these onto the tips of each of those diamonds, but what to call them? For constancy, and being able to use the character in filenames they’ll be @[2].

And now we have a bunch of hexes! This next step is going to be more of a personal choice, but for me, I like my base-level hexes to be 1 League, both because it’s a fun anachronistic number, and because it has pretty solid conversions to modern measurements (~3 miles and ~5 km) and it’s quite literally defined as being "The distance you can walk in an hour".
If you just make every hex 1 league across at this level, your planet has a circumference of ~130 km, which seems a bit small. If you like bigger hexes, this may be an OK planet size, but let me add another layer of depth. Remember that thing about hexagons infinitely tiling? Well turns out hexagons can (kinda) tile a hexagon!
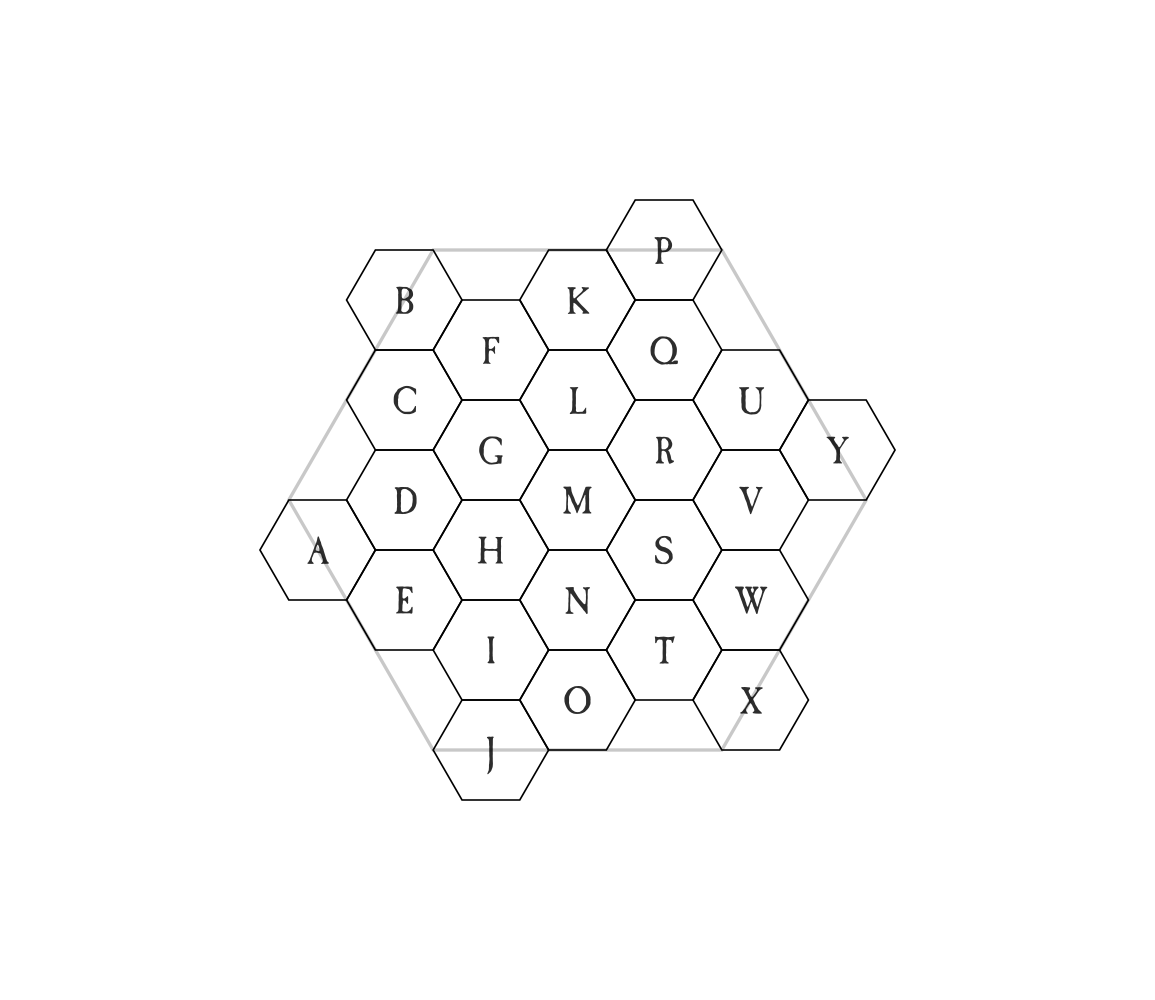
Now every "Atlas" hex is 5 Leagues, and we can fill out the smaller hexes… But ~650 km is still pretty small. Lets repeat it twice more to get around ~16,000 km which is not far off Mercury’s 15,000. Now we’ve got a reasonably sized world (going up one more hex size produces something twice the size of earth, which seems unreasonable).
What About the Pentagons?
Oh, right. we still have 12 pentagons that want to throw a wrench in our plans. Through the clever application of "Not worrying about it", we can treat pentagons as being hexagons with a slice taken out. For pentagons missing their top part, we eliminate hexes F, L, K and P. For pentagons missing their bottom part, we eliminate J, N, O, and T. In both cases, M becomes a pentagon as well. At the most zoomed in level, you can simply choose to make these pentagonal areas inaccessible (I put 2 at the poles) or just treat them as kinda weird hexes. Given that there’s only 12 of them on the planet, it shouldn’t come up much.
Wrap Up
Ok, what do we do with this?
You start populating hexes. Since everything has a name, it’s just a matter of filling in the blanks.
If you’re curious how to handle this in digital files, this is my file structure for my hexworld:
-
At the top level there are 10 folders labeled 0-9.
-
Inside each is 27 folders for each of the hexes in the panel
-
Inside each atlas hex is the 25 folders for the sub-atlas hexes
-
Another 25 for Region hexes and a final 25 for Local hexes.
-
A single file at each level is an overview of the important information for that hex, titled with it’s name (ex:
0LMT.md). -
I use inkscape for all my mapping, so I’ve also included maps at each layer made up of the maps at the next lowest layer.
You could alternately do this as a lot of binders with 0-9 and A-Z divider tabs.